Remember that frustrating feeling of staring at a complex automaton diagram, struggling to decipher its logic? I certainly do. I was once tasked with analyzing a convoluted Epsilon-NFA for a project, and I was lost in a maze of states and transitions. Thankfully, I discovered the power of converting that NFA into a more manageable DFA, simplifying the process and revealing the machine’s inner workings. This transformation, often described as a “de-fuzzification,” made the automaton readily understandable and made my job much easier. Today, I’m going to share the knowledge I gained through this experience and guide you through the process of epsilon NFA to DFA conversion, complete with solved examples that will illuminate the steps and help you master this fundamental concept in automata theory.

Image: www.studypool.com
Understanding Epsilon NFAs and DFAs
Let’s start by clarifying the difference between Epsilon NFAs (Non-deterministic Finite Automata) and DFAs (Deterministic Finite Automata). While both are state machines used to recognize patterns in input strings, they differ in how they handle transitions.
An Epsilon NFA is characterized by its ability to move between states without consuming any input symbol. These transitions are represented by the symbol ‘ε’, allowing for multiple possible paths within the automaton. On the other hand, a DFA is deterministic; for each state and input symbol, there exists exactly one transition. This deterministic nature simplifies analysis and implementation but can require a larger number of states to represent the same language.
Epsilon NFA to DFA Conversion: A Step-by-Step Guide
The conversion process consists of systematically transforming an Epsilon NFA into a DFA. The basic idea is to group the states of the NFA based on their ability to reach each other through epsilon transitions. This results in a simplified DFA with states representing groups of NFA states.
Here’s a detailed explanation:
- Identify the initial state of the NFA: This state serves as the starting point for the conversion process.
- Apply the Epsilon Closure operation: This operation finds all states reachable from the initial state using only epsilon transitions. The Epsilon Closure of a state S is the set of all states reachable from S by following epsilon transitions.
- Create the initial state of the DFA: The initial state of the DFA will be the Epsilon Closure of the initial state of the NFA.
- For each input symbol, compute the reachable states: For each input symbol, determine all possible states reachable from the current DFA state. This involves following transitions from the NFA states in the current DFA state and taking the Epsilon Closure of the resulting states.
- Create new DFA states for each reachable state set: Each distinct set of reachable states corresponds to a new DFA state. Mark the states as accepting if the NFA states within the set include an accepting state.
- Repeat steps 4-5 until no new DFA states are created: Continue this process, adding new DFA states as needed, until all possible input symbol transitions have been explored.
Illustrative Examples
Let’s solidify these steps with a couple of illustrative examples.
- **Example 1: Simple Epsilon NFA**
- **Example 2: Epsilon NFA with Multiple Transitions**
Imagine an Epsilon NFA with two states: State A (initial) and State B (accepting). There is an epsilon transition from State A to State B. In this case, the DFA would have two states: State 1 (corresponding to the Epsilon Closure of State A – it includes both State A and State B) and State 2 (corresponding to State B only). Since State B is an accepting state, State 1 and State 2 both become accepting states in the DFA.
Suppose we have a more complex Epsilon NFA with three states: State A (initial), State B, and State C (accepting). There are multiple epsilon transitions and regular transitions labeled with ‘a’ and ‘b’. The DFA would have more states, representing the possible state combinations reachable from the initial state through epsilon transitions and regular transitions. This DFA would have states like A, B, A, B, C, B, C based on the reachable states from the initial state.
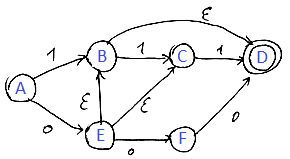
Image: www.pdfprof.com
Benefits of Epsilon NFA to DFA Conversion
Conversion to DFA offers numerous benefits:
- **Determinism:** Eliminating the ambiguity of epsilon transitions simplifies the automaton, making it easier to analyze and understand.
- **Simplicity:** The DFA, with its clear and concise structure, is easier to implement and use in practical applications.
- **Efficiency:** DFAs are well-suited for fast pattern recognition in applications like compiler design and text processing.
Tips for Successful Conversion
To ensure the successful conversion of your Epsilon NFA to a DFA, consider these tips:
- Understand the Input and Output:** Clearly define the language your NFA accepts and ensure the DFA you create recognizes the same language.
- Use a Systematic Approach:** Follow the step-by-step instructions provided earlier, and systematically explore each transition path.
- Visualize the Automata:** Draw diagrams of both the Epsilon NFA and the resulting DFA. Visual representation helps you understand the relationships between states and transitions.
Expert Advice: Focus on Language Equivalence
When performing the conversion, it’s essential to focus on language equivalence. This means ensuring the DFA you create recognizes the exact same language as the original Epsilon NFA. Double-check all possible input strings that your NFA accepts to verify that the DFA also accepts them.
FAQs Regarding Epsilon NFA to DFA Conversion
Here are some frequently asked questions about Epsilon NFA to DFA conversion:
- What are the specific cases where Epsilon NFA to DFA conversion is preferred?
- Is there a limit to the number of states in the resulting DFA?
- Can all Epsilon NFAs be converted into DFAs?
This conversion is often preferred when you need to implement the automaton for practical purposes, such as in a compiler or a text processing engine. Since DFAs are much easier to implement and analyze, they are often the preferred choice for these applications. Also, if you are using the automaton to implement a decision problem, such as deciding whether a given string is accepted by the automaton, it is often more efficient to use a DFA.
The number of states in the resulting DFA can vary depending on the complexity of the original Epsilon NFA. In the worst case, the number of states in the DFA can be exponentially larger than the number of states in the NFA. However, in practice, the number of states is often much smaller. The number of states in the DFA is directly related to the number of states in the NFA that are reachable from the initial state through epsilon transitions.
Yes, every Epsilon NFA can be converted into a DFA. The conversion process is guaranteed to produce a DFA that recognizes the same language as the original NFA. However, as mentioned, the resulting DFA might have a significantly larger number of states than the NFA.
Epsilon Nfa To Dfa Conversion Solved Examples Pdf
Conclusion
Epsilon NFA to DFA conversion is a powerful technique for simplifying automata and making them more readily applicable. By understanding the process, you equip yourself with a fundamental tool in automata theory. The ability to convert Epsilon NFAs and clearly understand the transition logic can significantly improve your ability to analyze and design complex systems. This conversion process is essential for understanding various computer science applications, particularly in areas like compiler construction and natural language processing.
Are you interested in diving deeper into this fascinating world of automata theory and exploring more practical examples of DFA conversion? Let us know!






